Sólidos

Na Geometria espacial temos os seguintes sólidos:

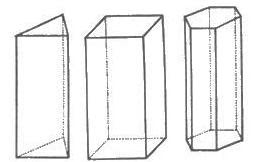
• Prismas

• Prisma de base quadrada: a base é um quadrado

Exemplo:

Dado um prisma cuja base quadrada possui uma aresta com 7 cm e seu comprimento é de 14 cm. Calcule a área total, e seu volume.
Resolução:

Primeiro vamos calcular a área da base:
Ab= 7² = 49 cm²
A figura da parte lateral é um retângulo e temos 4 deles, então calculamos a área e multiplicamos por 4:
Al=14 x 7 = 98 cm² x 4 = 392 cm²
A área total vai ser a soma destas duas áreas:
At=Ab+Al => At= 49+392=441 cm²
Agora o volume:
V= 49*14=686 cm³
Então temos: área total = 441 cm² e volume= 686 cm³

• Prisma de base triangular: a base é um triângulo

Exemplo:

Um sólido com a base que é um triângulo com aresta de 6 cm, tem 10 cm de comprimento, calcule o volume e mostre sua planificação.

Resolução:

Planificação:

Primeiro vamos calcular a área da base:

Ab=(6²√3)/4   => Ab= 9√3 cm²

V= 9√3*10 = 90√3 cm³

• Prisma de base hexagonal: a base é um hexágono

Exemplo:

Dado um prisma de base hexagonal com 2 cm de aresta e 15 de altura calcule a área total. (Adote √3=1,7)

calculando a area da base:

Ab=2²√3/4= √3cm² x 6= 6√3

calculando a area lateral:

Al= 15*2= 30 cm²

somando as áreas:

At=6√3+30cm²

At=10,2+30=40,2 cm²

• Cubo

O cubo é um paralelepípedo / prisma que possui todas as medidas iguais.

Exemplos:

1) Calcule o volume de um cubo com aresta de 5 cm.

Este exemplo dá para resolver de uma maneira lógica. O volume é dado em cm³ (neste caso cm) como todas as medidas são iguais é só elevar o 5 ao cubo, então:

V=5³= 125 cm³

2) As dimensões de um paralelepípedo retângulo são 9m, 6m e 4 m. Calcule a medida da aresta de um cubo cujo o volume é igual ao volume do paralelepípedo dado.

primeiro temos que calcular o volume do paralelepípedo:

V=9*6*4= 216

agora a gente tira raiz cúbica do volume do paralelepípedo

V= 6 cm :D

• Cilindro

O cilindro tem como base um círculo  e um retângulo lateral que tem como sua base a medida da circunferência do circulo.

Exemplos:

1) Determine a área lateral e a área total de um cilindro inscrito num cubo de aresta 4 cm.

Resolução:

Bom primeiro vamos calcular a área da base

o raio do circulo é a metade da medida da aresta do cubo, então:

Ab= pi(2²) => Ab=4pi

agora a area lateral:

Al=2*pi*2*4= 16pi cm²

agora a area total:

At= 4pi+16pi=20pi cm²

Anterior | Próxima